Why simpler?

In game development, simpler can mean a lot of things. With a physics engine, simpler usually refers to the complexity of the calculations. Complexity becomes more relevant after you identify the lowest common denominator for your game. Complexity, in terms of calculations, means that the processing may take longer or that the math for the physics may be difficult. To follow along with this article, you will not need a working knowledge of calculus.

Since JavaScript works well with HTML5 canvas, you'll often see physics applied to a canvas-based game. In some cases, such as a mobile platform like iOS or Android, the graphics from canvas become a dominating factor in your game. Building to a smaller resource platform means you need to squeeze as much processing as possible to leave enough room for the CPU to perform expensive graphics computations.

CPU utilization

Processing is the main reason to move from a well-tested, robust library to a home-grown, concise solution. The processing to be concerned about is called CPU utilization. CPU utilization is the amount of processing that's available, or that's being used, during your program's or game's runtime. Physics engines can take up as much CPU processing as the other parts of your game. Simpler choices mean less CPU utilization.

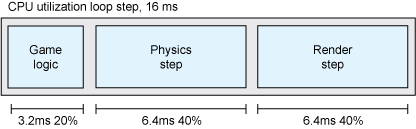
When running games, you typically aim for a target of 30-60 frames per second, which means your game's loop must fit within 33-16 milliseconds. The Example CPU utilization loop step shows an example. When a more complex solution is followed, it means compromising other features that may take up some of the CPU utilization of your game. Shaving off CPU usage from any of your game components, whenever possible, helps in the long run.

Example CPU utilization loop step

Deciding on the components

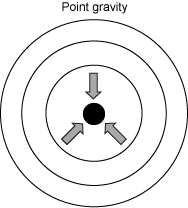
When using 2D, many different and elaborate effects can be emulated or faked, as long as you have an adequate handling of the engine. When building your game, consider what components you need. Decide which pieces you need to build out and which ones you can avoid forcing your engine to calculate completely. Things like point gravity, illustrated below, are harder to fake, while smaller hit areas can be easily accomplished.

Point gravity

Building a physics engine

This section discusses what makes up a physics engine and how to decide which features to include.

The first major step in building a physics engine is to choose the features and the order of operations. Deciding on the features may seem trivial, but the features help form the physics engine components and could indicate areas that might be difficult. For the example application, you'll build an engine to a game like the one shown below.

Platforming game

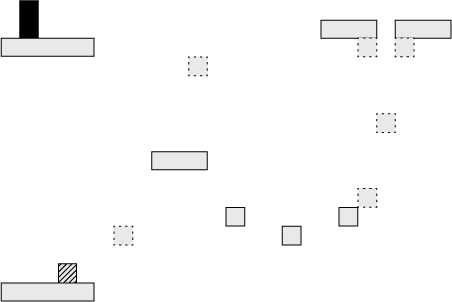
The boxes indicate:

• Player: Box containing diagonal lines
• Win condition, goal: Solid, black box
• Normal platform: Solid-line box
• Bouncy platform: Dashed-line box

Simple programmer graphics aside, you can visualize the features of the game. Players win when they reach the win condition/goal. The game is a platformer, so you'll need some of the most basic building blocks of a physics engine:

• Velocity, acceleration, and gravity
• Collision detection
• Bouncy collisions
• Normal collisions

The positional attributes will be used to drive the player. The collision detection will allow for the player to reach the goal and move around the game. The collision types will allow the game to have different ground types. By only having one player and essentially one dynamic object in the game, you can tone down the amount of collisions in the code.

Now that the game's features and the physics aspects of the features are identified, you can begin mapping out the physics engine structure.

Selecting the correct engine runtime

Physics engines come in two main forms: high-precision and real-time. High precision engines are used to simulate difficult or critical physics calculations; real-time engines are the types you see in video games. For the physics engine in the example, you'll use a real-time engine that infinitely runs its engine calculations until required to stop.

Real-time engines offer two options for controlling the physics engine timing:

• Static: Always provides the engine with a non-changing amount of time that is expected to pass every frame. Static real-time engines run at different speeds on different computers, so it's common that they behave differently.
• Dynamic: Feeds an elapsed time to the engine.

The example physics engine in this article needs to be running continuously, so you need to set up an infinite loop to run against the engine. This processing pattern is called the game loop. For this article, each one of the operations you'll run in that loop is called a step. Use the requestAnimationFrame API to use the dynamic option. The requestAnimFrame with polyfill section below shows the code required to run requestAnimationFrame. It uses a polyfill housed on the Khronos Group CVS Repository.

requestAnimFrame with polyfill

// call requestAnimFrame with a parameter of the
// game loop function to call
requestAnimFrame(loopStep);

Physics engine loop

Deciding on the order of operations within the loop might seem simple but it is not a trivial decision. While several different options are available for this step, you'll design the engine based on the features identified thus far, as shown in the Physics loop step.

Physics loop step

The section below shows that the step performs the calculation so that it does each type of calculation in a single pass. The other approach for this calculation would be to individually perform each object's calculations, but that generally produces odd results due to dependencies on other calculations.

Physics loop step pseudocode

1 User Interaction
2 Positional Logic
3 Detect Collisions
4 Resolve Collisions

Now that you have the workflow, the features, and a decision on the type of engine to build, you can start building the pieces.

Rigid body physics

Physics, as a science, is very vast and includes several different kinds of calculations. Newtonian physics makes up the common position, velocity, and acceleration calculations, while electromagnetism makes up magnets or electricity and can be used to emulate gravity in a physics system. Each of these areas of physics are great in their own right, but the level of complexity for those calculations goes beyond the scope of this tutorial.

When deciding on your physics system, the construction of the engine depends upon the type of calculations you want to do. The example engine will implement rigid body physics, or physics that does not deform. With rigid body physics you can avoid calculating force-based deformities that you would see in soft body dynamics or extra force modifications that you would see in any sort of multi-gravitational system.

Pieces of the engine

Physics engines are fairly complex computationally but are rather simple to structure once you know the pattern. The section Physics loop step pseudocode includes a high-level loop step pseudocode. Each calculation in that step can consist of its own object or API. The engine object graph consists of the following main components:

• Physics entity
• Collision detector
• Collision solver
• Physics engine

The entity, which is the object, body, or model that the engine acts upon, is the least active. The equivalent in Box2D is a b2Body class. The detector and solver work in concert by first finding collisions between entities and then passing over the collisions to the solver. Collisions are then converted into modifications applied to any entities the collisions are acting on.

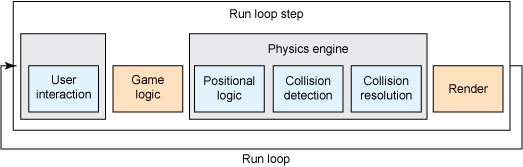
Physics engines, while encompassing the engine in its entirety, essentially manage, prepare, and communicate with each component through each phase in the system. The section below shows the relationship between each element in the physics engine.

Physics engine

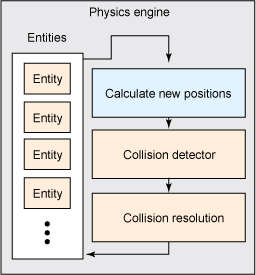
The four components make up the main force behind our engine. The first component you'll implement is the physics entity, which will represent every object on the screen.

Physics entity

Though the physics entity makes up the smallest and simplest of the components in the engine, it is the most important. As noted previously, the entity will represent each element on the screen. Entities, in both games and physics, represent the object's state by holding all the relevant metadata to that entity, as shown below.

Entity JavaScript object

// Collision Decorator Pattern Abstraction

// These methods describe the attributes necessary for
// the resulting collision calculations

var Collision = {

    // Elastic collisions refer to the simple cast where
    // two entities collide and a transfer of energy is
    // performed to calculate the resulting speed
    // We will follow Box2D's example of using
    // restitution to represent "bounciness"

    elastic: function(restitution) {
        this.restitution = restitution || .2;
    },

    displace: function() {
        // While not supported in this engine
           // the displacement collisions could include
        // friction to slow down entities as they slide
        // across the colliding entity
    }
};

// The physics entity will take on a shape, collision
// and type based on its parameters. These entities are
// built as functional objects so that they can be
// instantiated by using the 'new' keyword.

var PhysicsEntity = function(collisionName, type) {

    // Setup the defaults if no parameters are given
    // Type represents the collision detector's handling
    this.type = type || PhysicsEntity.DYNAMIC;

    // Collision represents the type of collision
    // another object will receive upon colliding
    this.collision = collisionName || PhysicsEntity.ELASTIC;

    // Take in a width and height
    this.width  = 20;
    this.height = 20;

    // Store a half size for quicker calculations
    this.halfWidth = this.width * .5;
    this.halfHeight = this.height * .5;

    var collision = Collision[this.collision];
    collision.call(this);

    // Setup the positional data in 2D

    // Position
    this.x = 0;
    this.y = 0;

    // Velocity
    this.vx = 0;
    this.vy = 0;

    // Acceleration
    this.ax = 0;
    this.ay = 0;

    // Update the bounds of the object to recalculate
    // the half sizes and any other pieces
    this.updateBounds();
};

// Physics entity calculations
PhysicsEntity.prototype = {

    // Update bounds includes the rect's
    // boundary updates
    updateBounds: function() {
        this.halfWidth = this.width * .5;
        this.halfHeight = this.height * .5;
    },

    // Getters for the mid point of the rect
    getMidX: function() {
        return this.halfWidth + this.x;
    },

    getMidY: function() {
        return this.halfHeight + this.y;
    },

    // Getters for the top, left, right, and bottom
    // of the rectangle
    getTop: function() {
        return this.y;
    },
    getLeft: function() {
        return this.x;
    },
    getRight: function() {
        return this.x + this.width;
    },
    getBottom: function() {
        return this.y + this.height;
    }
};

// Constants

// Engine Constants

// These constants represent the 3 different types of
// entities acting in this engine
// These types are derived from Box2D's engine that
// model the behaviors of its own entities/bodies

// Kinematic entities are not affected by gravity, and
// will not allow the solver to solve these elements
// These entities will be our platforms in the stage
PhysicsEntity.KINEMATIC = 'kinematic';

// Dynamic entities will be completely changing and are
// affected by all aspects of the physics system
PhysicsEntity.DYNAMIC   = 'dynamic';

// Solver Constants

// These constants represent the different methods our
// solver will take to resolve collisions

// The displace resolution will only move an entity
// outside of the space of the other and zero the
// velocity in that direction
PhysicsEntity.DISPLACE = 'displace';

// The elastic resolution will displace and also bounce
// the colliding entity off by reducing the velocity by
// its restituion coefficient
PhysicsEntity.ELASTIC = 'elastic';

Entity as a model

As the logic above shows, the physics entity stores nothing but raw data and produces different variants of the data set. If you're familiar with any of the MV* patterns, such as MVC or MVP, the entity represents the Model component of those patterns. (See Related topics for information on MVC.) The entity stores several pieces of data — all to represent the state of that object. For every step in the physics engine, those entities change, which ultimately changes the state of the engine as a whole. The different groupings of the entity's state data are discussed in more depth later.

You might have noticed that the entity in the Entity JavaScript object section does not include a render or draw function to display the entity on to the screen. By decoupling the physics logic and representations from the graphical representations, you can render out any graphical representation, thereby providing the power to skin the game entities. Despite the use of rectangles to represent the objects, as shown below, you aren't limited to rectangular images. Entities can have any image applied.

Bounding box and sprite

Position, velocity, and acceleration: The positional data

The entity includes positional data, which is information depicting how the entity can move in space. Positional data includes basic logic that you would see in Newtonian kinematic physics equations (see Related topics). Of these data points, the example entity is concerned about the acceleration, velocity, and position.

Velocity is the change in position over time, and, similarly, acceleration is the change in velocity over time. Calculating the change in position ends up being a fairly straightforward calculation, as shown below.

Position equation

p(n + 1) = v * t + p(n)

Where:

• p is the position of the entity. This is often represented with x and y.
• v is the speed or velocity. This is the amount of position change over time.
• t is the amount of time that passed. In JavaScript, this is measured in milliseconds.

Based on the equation above, you know that the entity's position will inevitably be impacted by the time applied to it. Similarly, the velocity is updated by acceleration, as shown below.

Velocity equation

v(n + 1) = a * t + v(n)

Where:

• v is the speed or velocity. This is the amount of position change over time.
• a is the acceleration of the entity. This is the amount of velocity change over time.
• t is the amount of time that passed. In JavaScript, this is measured in milliseconds.

Velocity equation is similar to Position equation, except that a represents the entity's acceleration. Though you won't be looping these equations into the entity's logic since it is meant to only store it, it's important to know what those parameters mean. You also need to consider the spatial representation of these entities.

Width and height: The spatial data

Spatial data refers to the parameters required to represent the hit area and space that the object takes. Elements such as shape and size affect the spatial data. For our example platform, you'll take a "smoke and mirrors" approach to the hit area. (Smoke and mirrors, a metaphor for deception or fraudulence, is based on magicians' illusions.)

It's common to use a hit area larger or smaller than the graphic or sprite representing the entity. Such hit areas often constitute a bounding box or rectangle. In the interest of simplicity and need for fewer calculations, the implementation will only use rectangles to test hit areas.

Rectangles, in graphics and physics, can be represented by four numbers. Use the upper left point for position, and use the width and height for size, as illustrated below.

Box representation

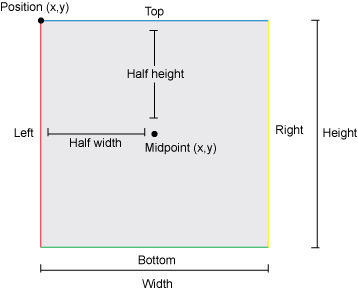
The bounding boxes only need position and size, as all other parameters are dependent on those components. Other calculations that also help are calculations for midpoints and edges, both of which are commonly used for collision calculations.

Restitution: The collision data

The final component of the entity is the collision data, or the information determining how the object should behave during collisions. For the example, collisions will include only displacement and elastic collisions, so the requirements are fairly limited, as shown below. The elastic collisions follow the naming patterns used in Box2D and define bounciness as restitution.

Fully elastic collision example

All of the data components provide the system with enough data to begin calculating all the changes that will occur over time in the example implementation.

Advanced collision concepts

The entity is sufficient for the example system, but there are often other parameters used for various collision solving. This section briefly discusses some of the other types.

Real-world values

In games, designers often model their worlds based on our world and measure things to the units in real-world space. Implementations that model their systems off of real world units, such as meters, only need a scale factor to convert their data points to and from these distances.

This tutorial doesn't provide an example of the conversions, but Box2D (see Related topics) provides a conversion ratio with supporting examples in several of their examples.

Mass and force

Mass and force make up a majority of physics engines, which might make you wonder why the example system does not. Because the example system does not require a mass, you can rely on the fact that force is a product of mass and acceleration and assume the mass is one unit. You can see this calculation below.

Force equation working out mass

// Our mass is always equal to one
var mass = 1;

// Force = mass * acceleration
var force = mass * acceleration;

// We can work the mass out of the equation
// and it won't change anything
force = acceleration;

The calculations are outside the scope of this tutorial. The sum of all forces, or the conservation of energy, are two physics calculations that you can use to calculate different collisions involving several moving entities rather than the singular entity used by the example system.

Shapes and concavity

The example system will support non-rotational bounding boxes, but sometimes more precise collision detection and solving are required. In some such cases, you should consider a polygonal approach, or include several bounding boxes to represent a single entity, as shown below.

Concave and convex

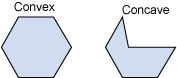
When a shape has a section broken out of it, you can end up with a shape that is concave. As shown above, concave shapes encompass shapes that have any side that pushes inwards towards the center. Concave shapes often require more precise and complex collision-detection algorithms. The other option, convex, are shapes that do not have any sides that push inward, toward the center. It is important to consider what kind of complexity your system will support when deciding on your shape support.

Collision detector

The second major step for the physics engine is the detection and resolution of collisions. A collision detector does exactly what the name implies. The collision detector for this tutorial will be simple and will include calculations to find whether a rectangle collides with another rectangle, but the objects often can collide with various types of objects, as shown below.

Collision detector collideRect test

// Rect collision tests the edges of each rect to
// test whether the objects are overlapping the other
CollisionDetector.prototype.collideRect =
    function(collider, collidee) {

    // Store the collider and collidee edges
    var l1 = collider.getLeft();
    var t1 = collider.getTop();
    var r1 = collider.getRight();
    var b1 = collider.getBottom();

    var l2 = collidee.getLeft();
    var t2 = collidee.getTop();
    var r2 = collidee.getRight();
    var b2 = collidee.getBottom();

    // If the any of the edges are beyond any of the
    // others, then we know that the box cannot be
    // colliding
    if (b1 < t2 || t1 > b2 || r1 < l2 || l1 > r2) {
        return false;
    }

    // If the algorithm made it here, it had to collide
    return true;
};

The following image shows the collision algorithm used to test the bounding boxes. The algorithm uses logic to determine if all of the edges are outside the bounds of the other rectangle in order to determine collision success. This collision detection doesn't support other shapes, but it's sufficient for illustration purposes.

Collision detection example

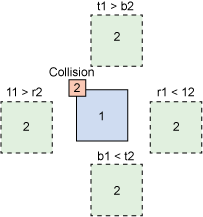
The single moving entity situation solves the issue of determining which objects to collide with. When building a collision-detection algorithm, it helps to prune off unnecessary entities.

Collision solver

The last part of the collision pipeline is the solver. Once a collision is encountered, entities must calculate their resolved location so the colliding entities are no longer colliding and the new directions are handled. In the example, you have objects that either completely absorb the force applied upon impact or reflect some of the force applied upon collision. The solver includes methods for the displacement calculations and for the elastic collisions mentioned previously.

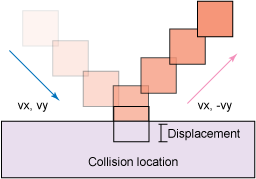
As shown below, the solver resolutions change the direction and position of the player. The example solver will first move the player back to the point where the collision first started in the direction from which the entity was coming.

Collision solve displacement diagram

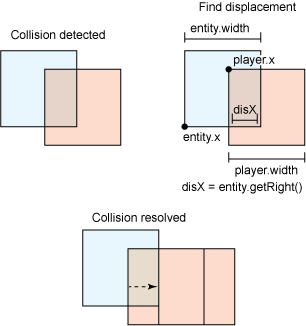
The solver equation will then modify the velocity of the entity. The displacement algorithm will remove the velocity, and the elastic one will use the restitution mentioned earlier to dampen and reflect the player's velocity, as shown below.

Displacement collision resolution

resolveElastic: function(player, entity) {
    // Find the mid points of the entity and player
    var pMidX = player.getMidX();
    var pMidY = player.getMidY();
    var aMidX = entity.getMidX();
    var aMidY = entity.getMidY();

    // To find the side of entry calculate based on
    // the normalized sides
    var dx = (aMidX - pMidX) / entity.halfWidth;
    var dy = (aMidY - pMidY) / entity.halfHeight;

    // Calculate the absolute change in x and y
    var absDX = abs(dx);
    var absDY = abs(dy);

    // If the distance between the normalized x and y
    // position is less than a small threshold (.1 in this case)
    // then this object is approaching from a corner
    if (abs(absDX - absDY) < .1) {

        // If the player is approaching from positive X
        if (dx < 0) {

            // Set the player x to the right side
            player.x = entity.getRight();

        // If the player is approaching from negative X
        } else {

            // Set the player x to the left side
            player.x = entity.getLeft() - player.width;
        }

        // If the player is approaching from positive Y
        if (dy < 0) {

            // Set the player y to the bottom
            player.y = entity.getBottom();

        // If the player is approaching from negative Y
        } else {

            // Set the player y to the top
            player.y = entity.getTop() - player.height;
        }

        // Randomly select a x/y direction to reflect velocity on
        if (Math.random() < .5) {

            // Reflect the velocity at a reduced rate
            player.vx = -player.vx * entity.restitution;

            // If the object's velocity is nearing 0, set it to 0
            // STICKY_THRESHOLD is set to .0004
            if (abs(player.vx) < STICKY_THRESHOLD) {
                player.vx = 0;
            }
        } else {

            player.vy = -player.vy * entity.restitution;
            if (abs(player.vy) < STICKY_THRESHOLD) {
                player.vy = 0;
            }
        }

    // If the object is approaching from the sides
    } else if (absDX > absDY) {

        // If the player is approaching from positive X
        if (dx < 0) {
            player.x = entity.getRight();

        } else {
        // If the player is approaching from negative X
            player.x = entity.getLeft() - player.width;
        }

        // Velocity component
        player.vx = -player.vx * entity.restitution;

        if (abs(player.vx) < STICKY_THRESHOLD) {
            player.vx = 0;
        }

    // If this collision is coming from the top or bottom more
    } else {

        // If the player is approaching from positive Y
        if (dy < 0) {
            player.y = entity.getBottom();

        } else {
        // If the player is approaching from negative Y
            player.y = entity.getTop() - player.height;
        }

        // Velocity component
        player.vy = -player.vy * entity.restitution;
        if (abs(player.vy) < STICKY_THRESHOLD) {
            player.vy = 0;
        }
    }
};

Above, the elastic collision uses a calculation to determine the overlap placement on the rectangle by checking the angle difference in direction between the player and the entity. The rectangles are normalized so that all calculations are handled as if the rectangle were a square. This kind of calculation is represented with the example in Collision solve displacement diagram. In this case, the resolver directly modifies the velocity. When dealing with multiple object collisions, be careful not to greedily set the velocity directly. Changing velocity due to multiple sources requires the use of energy-conservation equations and calculating the different angles and velocities.

The displacement algorithm is also used on the displacement calculation, with the exception that the velocity is set to zero rather than reflected and reduced.

Now that the components are outlined, the final step is to pull the system together in the engine.

Engine

The final component of the system is the engine itself, which is in charge of the workflow pseudocode (see the Physics loop step pseudocode section). The jobs of the engine generally match that of a controlling entity and include pushing content in and out of the collision components every loop step. The example engine's implementation manages the positional logic changes and the gravity before collisions are encountered, as shown below.

Physics engine

Engine.prototype.step = function(elapsed) {
    var gx = GRAVITY_X * elapsed;
    var gy = GRAVITY_Y * elapsed;
    var entity;
    var entities = this.entities;

    for (var i = 0, length = entities.length; i < length; i++) {
        entity = entities[i];
        switch (entity.type) {
            case PhysicsEntity.DYNAMIC:
                entity.vx += entity.ax * elapsed + gx;
                entity.vy += entity.ay * elapsed + gy;
                entity.x  += entity.vx * elapsed;
                entity.y  += entity.vy * elapsed;
                break;
            case PhysicsEntity.KINEMATIC:
                entity.vx += entity.ax * elapsed;
                entity.vy += entity.ay * elapsed;
                entity.x  += entity.vx * elapsed;
                entity.y  += entity.vy * elapsed;
                break;
        }
    }

    var collisions = this.collider.detectCollisions(
        this.player,
        this.collidables
    );

    if (collisions != null) {
        this.solver.resolve(this.player, collisions);
    }
};

Following the physics step, the engine first calculates the gravity and then applies it and the entity's acceleration to the velocity before calculating the entity's new x and y position. In the example, the collisions are produced by the collision detector's detectCollisions method. This detection method functions as a router to use the appropriate method (in this case, collideRect). Likewise, the solver uses the generic resolve method to transfer the call over to resolveElastic or its own displacement-resolver method.

While the engine in this implementation has a fairly trivial set of control, its usage is integral. In other engines, the engine may take a more front-seat role. In some cases, the engine will be sufficient for managing the physics step and the entities interacting in the physics engine. Beware of a common trap: don't allow the system to overshoot any possible collidable entities. If your entity moves further than the space a collidable entity takes up, your detector will completely ignore it.

Conclusion

When you build your own physics engine, implementing a simple solution for your game can work to your advantage. Though a robust solution is always more desirable, if you build a physics engine where computational complexity is important, or when building to a low processing device such as iOS or Android, you should consider a smoke-and-mirrors approach. When computational resources are low, solutions like those outlined in this tutorial are ideal.

Physics engines come with several parts to make them work. The most important parts are the entity, collision detector, collision solver, and engine core. By having the components working in unison, managing their own specific jobs, simple physics can be accomplished by selecting your shapes and algorithms with care. As long as you make appropriate decisions about your supported features, you can build a smaller subset of the more robust physics engine implementations. The more robust physics engines can always help drive your own to determine the best approach for your own game.